2026 수능 수학 고난도 문항 대비법
2026.01.152026학년도 대학수학능력시험 수학 영역은 단순한 '풀이 기술'을 넘어 '개념의 연결과 통합 사고력'을 평가하는 흐름을 명확히 했습니다. 이번 수능 수학 분석을 통해 초등 시기부터 준비해야 할 필승 전략을 정리해보았습니다.
1. 2026 수능 수학 총평
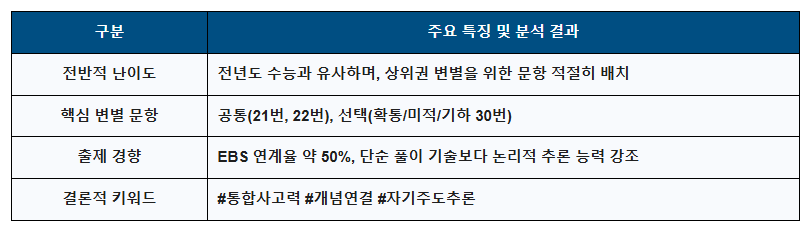
2. 2026 수능 수학, 무엇이 승패를 갈랐나? 고난도 문항 분석
Q1. 가장 어려웠던 문항과 그 이유는 무엇인가요?
단순 계산이 아닌, 극한값이 존재하기 위한 조건을 해석하고 새로운 함수의 형태를 추론해야 하는 복합 사고형 문제였습니다.

Q2. 최근 수능 수학의 변화 패턴은?
2026학년도 수능 수학은 문제풀이 기술보다는 개념과 성질을 활용하여 해결하는 문항으로 구성되었습니다.
즉, 과거처럼 공식을 대입해 기계적으로 푸는 학생보다, 3~4개의 교과 개념을 유기적으로 엮어 상황을 해석할 줄 아는 학생에게 유리했습니다.
Q3. 초등학생, 앞으로 수능 수학 어떻게 대비해야 할까?
수능 수학의 고난도 문항을 해결하는 힘은 초등 과정의 '개념 확장 습관'에서 시작됩니다.
또한, 복잡하고 새로운 문제를 만났을 때도 내가 무엇을 구해야 단계적으로 나누어 생각해 보는 연습이 중요합니다. 즉, 개념에 대해 충실히 이해하고 통합적인 사고력을 키워야 하는 것이죠.
3. 통합 사고력의 해답, 윤선생 '큐리매쓰(Curimath)'
윤선생이 만든 통합 사고력 수학 ‘큐리매쓰’는 수능까지 이어지는 탄탄한 수학 실력을 위해 다음과 같은 솔루션을 제공합니다.1) 개념은 완벽하게! 자연스럽게 심화학습까지 정복!

통합적인 수학 사고력이 형성되려면 단계적 절차와 확장이 필요합니다. 윤선생 큐리매쓰는 세 가지 학습 구조도를 갖고 있습니다.
Step 1: 다양한 소재의 문제를 통해 개념을 완전히 체득합니다.
Step 2: 배운 개념을 스스로 활용해 응용 문제를 해결하는 힘을 기릅니다.
Step 3: 아는 개념을 다른 영역으로 확장해 자연스럽게 고등 심화 수학에 대비합니다.
2) 질문을 통해 생각하는 힘을 키우는 '질문형 학습'
큐리매쓰는 단순히 정답을 알려주지 않습니다. 꼬리에 꼬리를 무는 질문을 통해 아이가 직접 논리적 근거를 찾아 답을 구하도록 유도합니다. 이 과정이 쌓여 수능의 고난도 추론 문항을 해결하는 근육이 됩니다.
3) 초·중·고를 하나로 잇는 '계통 수학' 콘텐츠 큐리매쓰는 초·중·고 수학에서 기본이 되는 개념을 연결해주는 [개념 브릿지]와 초·중·고 수학의 6개 영역을 완성시켜주는 [개념 컴플릿]로 구성되어, 초등에서 알고 있는 개념들을 중·고등 수학으로 확장시켜 줍니다.
큐리매쓰는 초·중·고 수학에서 기본이 되는 개념을 연결해주는 [개념 브릿지]와 초·중·고 수학의 6개 영역을 완성시켜주는 [개념 컴플릿]로 구성되어, 초등에서 알고 있는 개념들을 중·고등 수학으로 확장시켜 줍니다.
예를 들어, [개념 브릿지]로 수학의 형식화, 기호화를 연습한 초·중등 학생들은 고등 수학 개념인 <수와 식>, <함수>, <도형>, <수열>, <미적분>, <확률과 통계>를 처음 접하더라도 배운 내용과 결합하여 매끄럽게 문제를 해결할 수 있습니다.
4. 큐리매쓰 수학 공부 후기

2026 수능이 준 메시지는 명확합니다. "자기주도적으로 개념을 결합하고 확장할 수 있는가?"
공식만 외우는 학습은 더 이상 고득점을 보장하지 않습니다. 초등 시기부터 윤선생 큐리매쓰와 함께 '생각하는 힘'을 길러주세요. 어떤 난이도에도 흔들리지 않는 통합 사고력이 아이의 미래를 바꿉니다.
